 | |||||||||||||||||||
|
שמואל בראל (MBA, ME, BSc) יועץ מומחה לפיתוח עסקי ליזמים וחברות סטארט אפ צעירות, לגיוס הון התחלתי משלב הרעיון ועד להשקעת סיד.
צור קשר!
  עדכון אחרון: 29 במאי 2016  האתגרים בגיוס הון ראשוני לסטארט אפ בשלבי הפרה-סיד והסיד
האתגרים בגיוס הון ראשוני לסטארט אפ בשלבי הפרה-סיד והסידמימון בתוכנית עסקית השלב השני בכתיבת הפרק הפיננסי בתוכנית העסקית הוא להעביר סכומי כסף שמתקבלים בזמנים שונים לתקופת זמן מסוימת באמצעות היוון בשיעור ההון. היוון הוא הפעולה הפיננסית הבסיסית ביותר בכל תוכנית מימון. פורטל שיווק • עקרונות בשיווק עסקי • מחקר שיווקי וסקרי שוק • ניתוח התנהגות צרכנים • מבנה השוק וניתוח התחרות • פילוח שוק ובחירת קהל מטרה • תמהיל השיווק • תהליך שיווק למוצר חדש פורטל הנדסה • תכן הנדסי של מוצר חדש • דירוג צרכי לקוחות • הגדרת מפרט ביצועים • בעיות בסיסיות ועקרונות פתרון • יצירת חלופות (קונספט) • בחירת חלופות תכן ראשיות • ארכיטקטורה ותכן על • בחירת החלופה למימוש פורטל אסטרטגיה • עקרונות באסטרטגיה עסקית • ניתוח כוחות חיצוניים • ניתוח כוחות פנימיים • אסטרטגיות מיצוב ויתרון תחרותי • יריבות ודינאמיקת התחרות • אסטרטגיות צמיחה • אסטרטגיה בינלאומית פורטל ניהול • ניהול הארגון • מנהיגות • קבלת החלטות • מבנה ארגוני • ניתוח וניהול סיכונים • תכנון פרויקט פורטל מימון • מימון ותוכנית פיננסית • מעבר בין ריביות ותקופות • היוון תזרימי כספים • מדדים כלכליים • דוחות כספיים • שיטת היוון תזרים מזומנים • ניתוח עלות מחזור חיים • כתיבת תוכנית פיננסית |
היוון תזרימי כספים
מימון הוא מכלול הפעולות שאנשים וארגונים נוקטים בהם כדי לנהל את כספם, או על מנת לגייס כספים כדי לממש פרויקטים שהם מעונינים לבצע. מבוא: מימון ותוכנית פיננסית 1. מעבר בין ריביות ותקופות 2. היוון תזרימי כספים 2.1 היוון בריבית תקופתית קבועה 2.2 היוון בריבית תקופתית משתנה 2.3 היוון לתקופות באורך משתנה 2.4 היוון תזרים אינסופי 2.5 היוון תזרים שגדל בקצב קבוע 3. מדדים כלכליים להערכת פרויקטים 4. חשבונאות פיננסית: דוחות כספיים 5. הערכת שווי בשיטת היוון תזרים מזומנים 6. ניתוח עלות מחזור חיים 7. כתיבת תוכנית פיננסית 2. היוון תזרימי כספיםתזרים מזומנים כספי הצפוי מפרויקט מסוים עשוי להגיע בסכומים משתנים ומרווחי תקופות לא זהות. היוון תזרימי כספים (Present Value of Cash Flows) היא השיטה לחישוב הערך הנוכחי של תזרים עתידי שמהוון במחיר הון כלשהו.הגישה היא "מלמעלה למטה" - מחיר ההון הוא ידוע, ואנו רוצים לדעת מהו הערך הנוכחי של התזרים העתידי הצפוי. סימון התזרים הכספי בתקופה נעשה באמצעות CFT : PVT = השווי המהוון של התזרים העתידי CFT = סכום התזרים הכספי העתידי T = התקופה שבה הגיע התזרים i = הריבית התקופתית 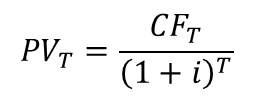 היוון של תזרים עתידי היוון בריבית תקופתית קבועה כאשר רוצים לחשב מהו הערך הנוכחי של סדרה של תזרימים עתידיים שמגיעים במועדים שווי-הפרשים, וגובה התזרימים שונה, אך ריבית ההיוון זהה, פשוט מהוונים כל אחד מהתזרימים לפי התקופה שבה הוא צפוי להתקבל; סכימה של כל התזרימים המהוונים היא הערך הנוכחי: 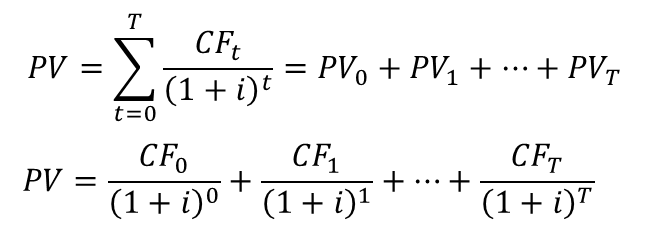 ערך נוכחי של תזרימים עתידיים דוגמא: הריבית התקופתית היא 6%. מה הערך הנוכחי של תזרים עתידי שמשלם היום 1,000 ש"ח, בתום התקופה הראשונה 1,400 ש"ח, ובתום התקופה השנייה 1,900 ש"ח? 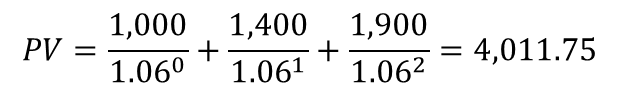 היוון בריבית תקופתית משתנה אחת מההנחות בשווקים הפיננסיים היא שככל שסכום כסף מופקד לזמן ארוך יותר, התשואה שידרוש המפקיד תהיה גבוהה יותר, בשל הפסד הנזילות - המפקיד לא יכול להשתמש בכסף במשך זמן רב, ודורש תוספת פיצוי. היוון תזרים עתידי עשוי להתבצע גם בריביות שמשתנות מתקופה לתקופה. המשקיע דורשת פרמיה עבור חוסר הנזילות. המבנה העתי של שערי הריבית (Term Structure Of Interest Rates) הוא עקום שמתאר את הריביות התקופתיות לאורך ציר הזמן. מבחינים בין שלוש סוגים של ריביות, שקשורות אחת בשניה: • ריבית שולית (forward): זו הריבית בכל תת-תקופה, לתקופה עצמה • ריבית ממוצעת (spot): הריבית התקופתית הממוצעת לתקופה, לכלל התקופות • ריבית מצטברת (total): הריבית המצטברת לכלל התקופות איך מחשבים את הקשרים בין הריביות? נאמר שבתקופה הראשונה צפויה לשרור ריבית בגובה r1, בתקופה השנייה ריבית בגובה r2, וכך הלאה עד התקופה ה-nית. איך מחלצים את הריבית הממוצעת והמצטברת? 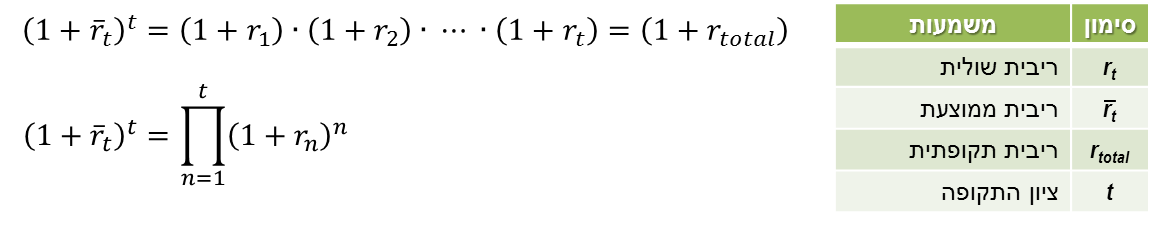 חישוב מבנה עתי של שערי ריבית דוגמא: הריבית הצפויה לשנה הקרובה היא 5%, לשנה השניה 6%, ולשנה השלישית 7%. מהו הערך הנוכחי של 1,000 ש"ח שיתקבלו בעוד 3 שנים? מהי הריבית הממוצעת לכל תקופה? מהי הריבית המצטברת לשלוש שנים? 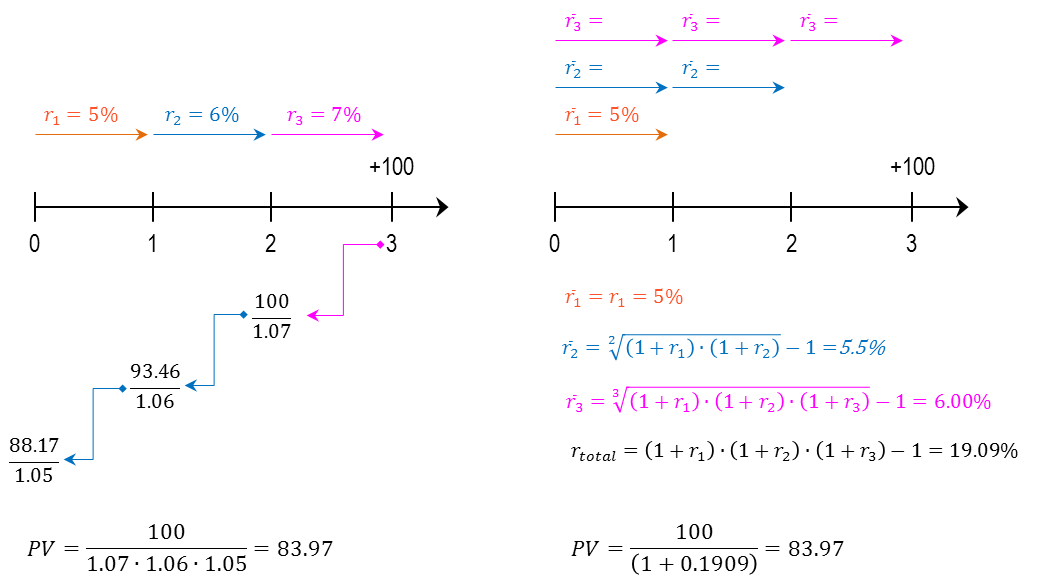 דוגמא - היוון סכום בריבית תקופתית משתנה דוגמא: הריבית הצפויה לשנה הקרובה היא 5%, לשנה השניה 6%, ולשנה השלישית 7%. מהו הערך הנוכחי של תזרים שבו 100 ש"ח יתקבלו בעוד שנה, 100 ש"ח יתקבלו בעוד שנתיים, ו-100 ש"ח יתקבלו בעוד שלוש שנים? 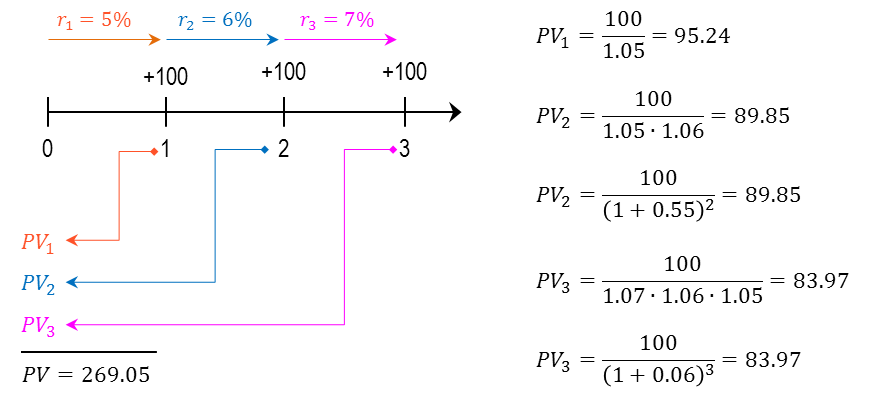 דוגמא - היוון תזרים בריבית תקופתית משתנה היוון לתקופות באורך משתנה ייתכן מצב שבו חלק מהתזרימים לא מגיעים בהפרשי זמן שווים: למשל, תזרים עם ריבית של 5%, שמניב 100 ש"ח בתום כל אחת משלוש השנים הראשונות, ולאחר עוד חצי שנה מניב 50 ש"ח. מה הערך הנוכחי של תזרים כזה? אופן החישוב נעשה באופן הבא: הריבית התקופתית היא 5%, והתקופות בהן מתקבל התזרים הן: 1, 2, 3, 3.5. לאחר שמתרגמים את התקופות לבסיס תקופתי זהה, מהוונים את הסכום לפי התקופות המתוקננות: 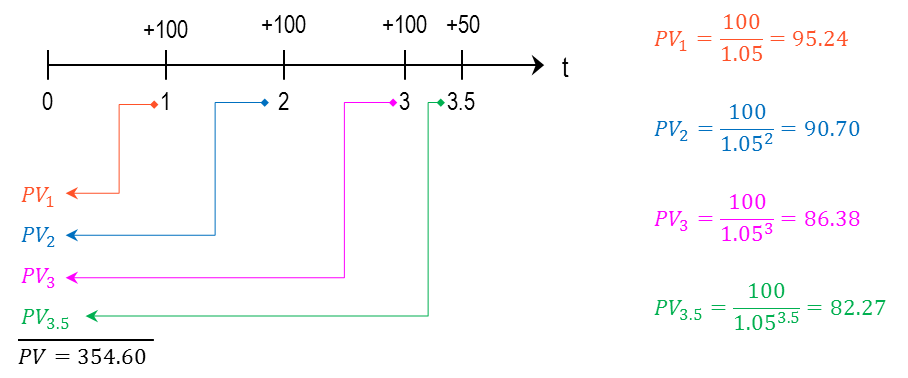 דוגמא - היוון לתקופות באורך משתנה היוון תזרים אינסופי תזרים אינסופי (קונסול) הוא תזרים שמניב הכנסה תקופתית קבועה. כדי להוון תזרים כזה החישוב נעשה באמצעות טור הנדסי מתכנס. מניית בכורה היא דוגמא לקונסול: היא מבטיחה דיבידנד בגובה קבוע לנצח. נניח שאפשר לרכוש נכס שמניב 100 ש"ח בכל תקופה לנצח. התשואה שניתן להשיג עבור נכס ברמת סיכון דומה היא 6%. הערך הנוכחי הוא היוון של 100 ש"ח בריבית של 6% מתקופה 1 ועד אינסוף. החישוב בפועל מתבצע באופן הבא: 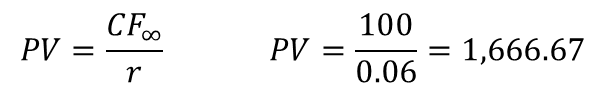 דוגמא - היוון תזרים אינסופי באופן דומה, אם מציעים לרכוש נכס במחיר של 1,666.67 ש"ח, והנכס מניב בכל תקופה 100 ש"ח - לנצח, התשואה הגלומה בנכס היא 6% לתקופה. היוון תזרים שגדל בקצב קבוע סוג נוסף של תזרים הוא תזרים שמניב סכום קבוע בתקופה הראשונה, והסכום הקבוע עולה בשיעור צמיחה קבוע g% בכל תקופה. חישוב מחיר מניה באמצעות מודל הדיבידנדים של גורדון הוא דוגמא ל-היוון תזרים שגדל בקצב קבוע. נניח שאפשר לרכוש נכס שמניב 100 ש"ח בכל תקופה, לנצח, וגם שיעור הצמיחה של הנכס (שווי הנכס) עולה ב- 1% בכל תקופה. אם התשואה שניתן להשיג עבור נכס ברמת סיכון דומה היא 6%, החישוב נעשה באופן הבאה: 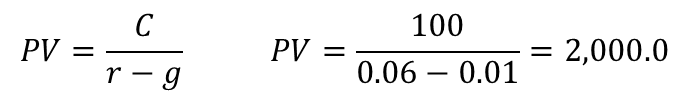 דוגמא - היוון תזרים אינסופי שגדל בקצב קבוע באופן דומה, איך אפשר לחשב את המחיר של מניה, שהדיבידנד האחרון שחולק היה 1 ש"ח, הדיבידנד התקופתי גדל בשיעור של 0.5% בשנה, והתשואה שדורשים בעלי המניות ממניות דומות הוא 9% לשנה? במקרה זה, המונה הוא הדיבידנד התקופתי הבא, ומחיר המניה: 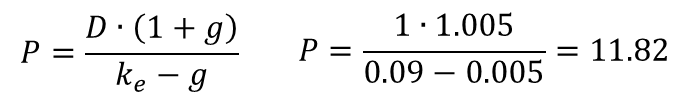 דוגמא - מודל הדיבידנדים של גורדון |
www.SamsProjects.co.il