תוכנית עסקית | מימון ותוכנית פיננסית - מעבר בין ריביות ותקופות

מעבר בין ריביות ותקופות

מימון הוא מכלול הפעולות שאנשים וארגונים נוקטים בהם כדי לנהל את כספם, או על מנת לגייס כספים כדי לממש פרויקטים שהם מעונינים לבצע.

מימון ותוכנית פיננסית
1. מעבר בין ריביות ותקופות
1.1 ריבית
1.2 תשואה
1.3 מחיר הון
1.4 מעבר בין ריביות
1.5 חישובי ערך נוכחי וערך עתידי
2. היוון תזרימי כספים
3. מדדים כלכליים להערכת פרויקטים
4. חשבונאות פיננסית: דוחות כספיים
5. הערכת שווי בשיטת היוון תזרים מזומנים
6. ניתוח עלות מחזור חיים
7. כתיבת תוכנית פיננסית

1. מעבר בין ריביות ותקופות

שמו של מחיר ההון נגזר מזהות הצד הפיננסי בעסקה: צד שמלווה כסף יגבה עבורו אחוזי ריבית (Interest); צד שביצע השקעה יחשב את שיעור התשואה (Return); מי שלווה כסף מיותר ממקור אחד, וגם משתמש בהון עצמי לצורך מימון פרויקט, מהוון את התזרים העתידי ב-מחיר ההון (Cost of Capital).

מחיר ההון כולל בתוכו שני מרכיבים: ריבית חסרת-סיכון, ופרמיית סיכון ספציפית לעסקה. ריבית חסרת-סיכון היא התשואה שניתן לקבל תמורת תזרים עתידי "וודאי" - למשל, אגרת חוב ממשלתית. הפרמיה על הסיכון תלויה בוודאות התזרים - עד כמה בטוח ספק ההון שיקבל את סכומי התזרים שנקבעו במועד, ובסכום. ככל שאי-הוודאות של התזרים העתידי גבוהה יותר, הסיכון שבקבלת הכסף בחזרה גבוה יותר, ולכן הפרמיה שידרוש ספק ההון גדולה יותר.

ריבית
ריבית היא סכום הכסף הנוסף שמשלם הלווה (מקבל הכסף) ל--מלווה (ספק הון) בתמורה לזכות שנותן המלווה ל-לווה להשתמש בסכום כסף מסוים (קרן ההלוואה) למשך תקופה מסוימת (תקופת הלוואה); ריבית היא מחיר השימוש בכסף מושאל.

• ריבית פשוטה - ריבית המשולמת כאחוז מסוים מהקרן
• ריבית דריבית - ריבית המחושבת על הקרן וגם על תשלום הריבית האחרון

ריבית עשויה להיות נקובה בערך שנתי, אך מועדי התשלום שלה עשויים להיות קצרים יותר - בכל חודש, בכל 3 חודשים, פעמיים בשנה, למשל. במקרה זה, הנוסחא לחישוב תשלום הריבית נתונה בצורה הבאה: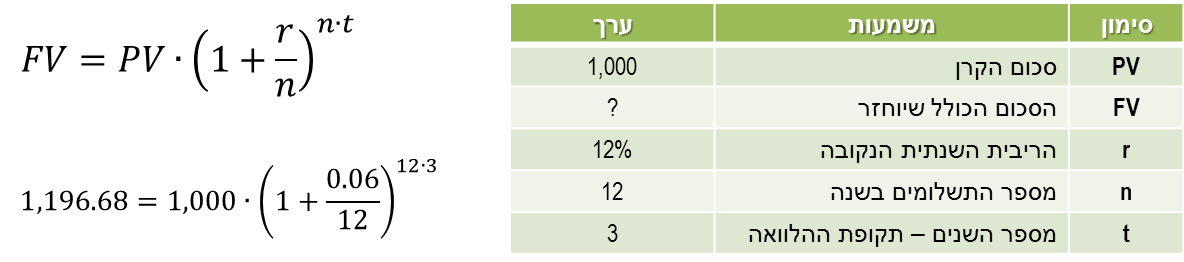

דוגמא - חישוב הערך העתידי של התחייבות

לרוב, מה שמעניין ת'כלס הוא מהו גובה התשלום החודשי שיש להחזיר עבור הלוואה שנלקחת היום, למשך מספר תקופות. במקרה כזה, משתמשים בנוסחה של ערך נוכחי של סדרה קבועה (אנונה). עבור הדוגמא לעיל, נאמר שאנו רוצים לקבל היום 1,000 ש"ח למשך 3 שנים, בריבית נקובה של 12% לשנה, אבל החזר ההלוואה נעשה בכל חודש: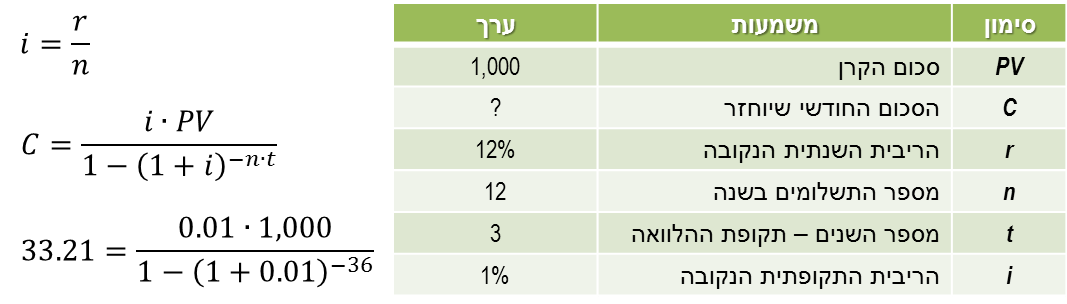

דוגמא - חישוב החזר התשלום החודשי של הלוואה

משתי הדוגמאות האלו אפשר ללמוד שסך כל תשלומי הריבית עבור ההלוואה הם בגובה 196.68 ש"ח (היום); ההחזר החודשי למשך שלוש שנים יהיה בגובה 33.21 ש"ח.

תשואה
תשואה היא היחס בין שווי השקעה בשתי נקודות זמן שונות, בד"כ שנה. לרוב התשואה תוצג באחוזים כ- שיעור התשואה.

מהו שיעור התשואה של פרויקט שהושקעו בו 100 ש"ח, ולאחר שנה התקבול היה בגובה 120 ש"ח? שיעור התשואה של הפרויקט הוא 20%: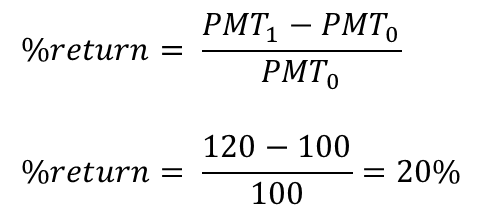

דוגמא - חישוב תשואה תקופתית

מה הוא שיעור התשואה החודשית? המשמעות של שיעור תשואה חודשית הוא שיעור תשואה כזה, שאם נשקיע את את 100 השקלים הראשונים בשיעור התשואה החודשי בחודש הראשון, ונשקיע את הקרן והתקבול הראשון בשיעור תשואה זהה בחודש השני, וחוזר חלילה למשך 12 חודשים, נקבל סכום כולל של 120 ש"ח.
נוסחאת ההמרה בין תקופות שונות של תשואות זהה לנוסחאת ההמרה בין תקופות שונות של ריביות, בהנחה של ריבית דריבית: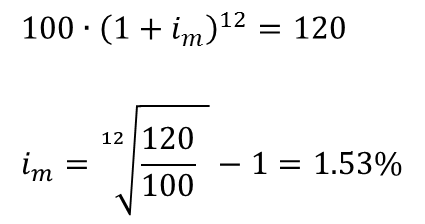

דוגמא - מעבר מתשואה שנתית לחודשית

מחיר ההון
הדרך המהירה והפשוטה ביותר להסביר את מושג מחיר ההון הוא בדוגמא הבאה: יש לך 100 ש"ח שאתה רוצה להשקיע: אפשר להשקיע אותם בפק"מ בבנק, להשקיע ברכישת אגרת חוב, להשקיע ברכישת מניה, להשקיע בהקמת עסק פרטי.

פרופיל הסיכון של כל אחת מאלטרנטיבות ההשקעה שונה: הפק"מ נחשב לכלי השקעה חסר-סיכון; אגרת-חוב נחשבת לבטוחה יחסית; מניה נחשבת לנכס מסוכן; השקעה בעסק פרטי מסוכנת יותר מכל האפשרויות האחרות.

השאלה היא: תמורת איזה סכום עתידי, נאמר בעוד שנה, תסכים להיפרד מ- 100 ש"ח היום? המשקיע הראציונלי ידרוש לקבל סכום גבוה יותר ככל שפרופיל הסיכון של ההשקעה גבוה יותר - כלומר, ככל שאי-הוודאות בנוגע לשווי סכום ההשקעה בעתיד (קרן) גבוה יותר, המשקיע ידרוש פיצוי כספי גבוה יותר.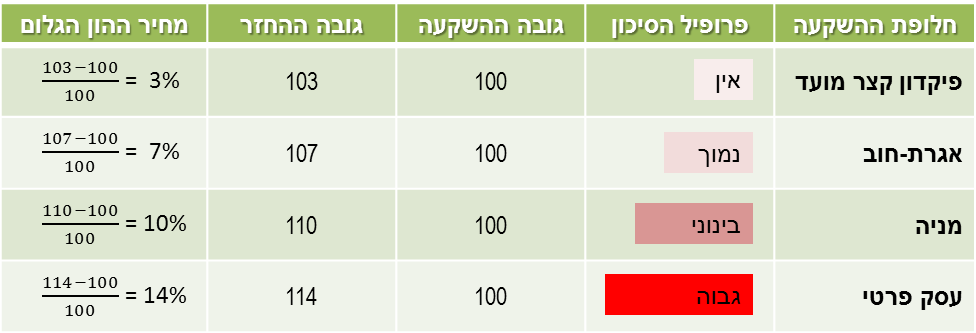

דוגמא - מחיר ההון (תשואה) גדלה עם הסיכון

לפירמה שלווה כסף באמצעות הנפקת מניות ומכירת אגרות חוב נהוג לחשב את מחיר ההון המשוקלל (WACC = Weighted Average Cost of Capital) - זהו ממוצע משוקלל של התשואה שדורשים בעלי המניות והריבית שדורשים רוכשי אגרות החוב.

מעבר בין ריביות

ריבית נומינלית (ריבית חוזית, ריבית קונטוקורנטית, ריבית נקובה) היא הריבית הנקובה במסמכי מתן ההלוואה, ללא התחשבות במועדי חיוב הריבית ובהיטלים הנלווים (עמלות). בדרך כלל תצויין הריבית לתקופה של שנה אחת.
ריבית אפקטיבית (ריבית מתואמת) היא הריבית המשולמת בפועל על ההלוואה, תוך שקלול מועדי חיוב הריבית וההיטלים הנלווים (עמלות ותשלומים אחרים).

דוגמא: לקחת הלוואה של 1,000 ש"ח היום, בריבית נקובה של 12% לשנה. אם ההחזר נעשה רק פעם אחת, בתום השנה, אזי הריבית האפקטיבית היא 12%. מהי הריבית האפקטיבית אם החזר ההלוואה נעשה בכל חודש?

הריבית החודשית הנקובה היא 1%. מכאן, בחישוב של ריבית דריבית של ריבית של 1% לחודש למשך 12 חודשים, נקבל שהריבית האפקטיבית היא: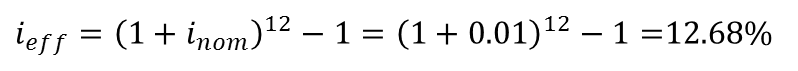

דוגמא - מעבר מריבית נומינלית לריבית אפקטיבית

ריבית ריאלית היא ריבית נומינלית שמותאמת לשינוי במדד כלשהו (אינפלציה, מדד המחירים לצרכן, מדד תשומות הבניה, וכיוצא בזה). חישוב הריבית הריאלית נעשה באמצעות נוסחאת פישר:

דוגמא - חישוב ריבית ריאלית

חישובי ערך נוכחי וערך עתידי
כדי לחשב את השווי הנוכחי ואת השווי העתידי, צריך להוון את התזרים העתידי הצפוי בשיעור ההון (הריבית).

• ערך נוכחי (PV = Present Value), הוא השווי היום של תזרים עתידי צפוי כלשהו.
• ערך עתידי (FV = Future Value), הוא השווי בעתיד של תזרים עתידי צפוי כלשהו.

דוגמא - ערך נוכחי:
מה הערך הנוכחי של 5,000 ש"ח שיתקבלו בעוד תקופה, בריבית תקופתית של 10%? מה יהיה הערך הנוכחי בעוד שנתיים? ... 10 שנים?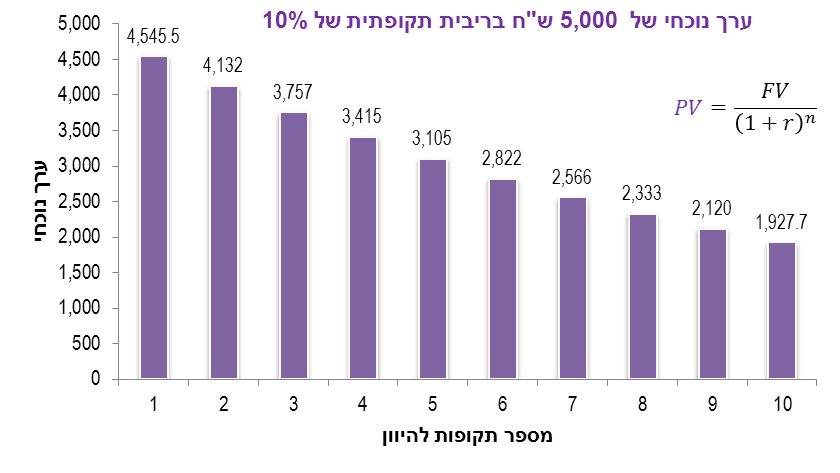

דוגמא - חישוב ערך נוכחי

דוגמא - ערך עתידי:
מה הערך העתידי של 1,000 ש"ח שיתקבלו בעוד תקופה, בשיעור תשואה של 10%? מה יהיה הערך העתידי בעוד שנתיים? ... בעוד 10 שנים?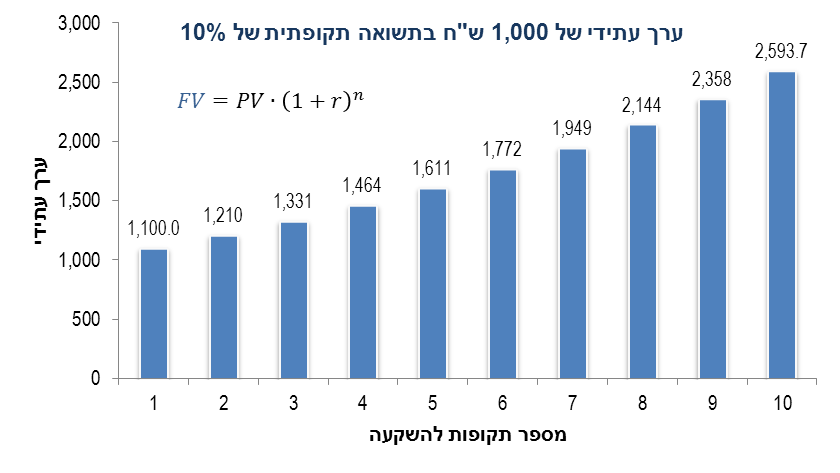

דוגמא - חישוב ערך עתידי

דוגמא: חישוב שיעור הריבית הגלום
מה שיעור הריבית (/תשואה) הגלום לתקופה, ב-10,000 ש"ח היום, שהערך העתידי שלהם בעוד 5 תקופות הוא 15,000 ש"ח?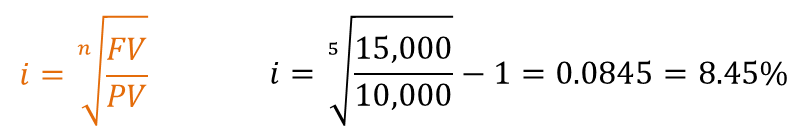

דוגמא - חישוב שיעור ריבית גלומה

דוגמא: חישוב מספר התקופות מצטברות
כמה תקופות השקעה מצטברות (רבית דריבית) יש להשקיע סכום של 500 ש"ח כדי לקבל 1,000 ש"ח, בשיעור תשואה של 6% לתקופה?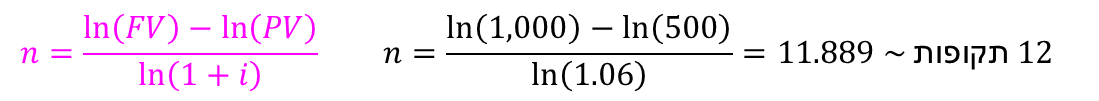

דוגמא - חישוב מספר התקופות מצטברות